Post History
The peak is about 55 It looks like, based on this Anydice calculation that peak skill increase is about 55. I haven't done an analytical calculation of the probabilities, but my guess is that the...
Answer
#3: Post edited
by
pureferret
·
2023-10-30T02:12:03Z (7 months ago)
- ## The peak is about 55
It looks like, based [on this Anydice calculation](https://anydice.com/program/32abc) that peak skill increase is about 55.- I haven't done an analytical calculation of the probabilities, but my guess is that the initial pass (under) and then the skill advancement check (over) make the distribution symmetric.
- That is a skill level of 5 (where the probability of a success then a subsequent skill advancement is 0.05×0.95=0.0475) is equivalent to when the skill level is 95 (i.e. 0.95×0.05=0.0475), but for a skill level of 50 (i.e. 0.5×0.5=0.25).
- But the probability contribution from both the penalty die, and needing to initially roll under ⅕ the make higher rolls very slightly 'better' but not to completely break the underlying symmetry and stop the much higher rolls being worse.
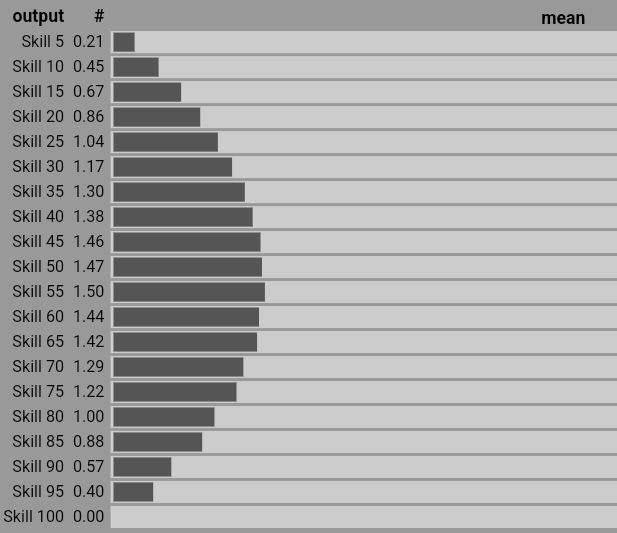
- Here's a visual representation of that distribution, but you need to look at the numbers to see subtle shift to larger values:
- 
Although, it looks like the balance shifts downwards for repeated rolls at the same skill level: https://anydice.com/program/32abe
- ## The peak is about 55
- It looks like, based [on this Anydice calculation](https://anydice.com/program/32abc/summary/table) that peak skill increase is about 55.
- I haven't done an analytical calculation of the probabilities, but my guess is that the initial pass (under) and then the skill advancement check (over) make the distribution symmetric.
- That is a skill level of 5 (where the probability of a success then a subsequent skill advancement is 0.05×0.95=0.0475) is equivalent to when the skill level is 95 (i.e. 0.95×0.05=0.0475), but for a skill level of 50 (i.e. 0.5×0.5=0.25).
- But the probability contribution from both the penalty die, and needing to initially roll under ⅕ the make higher rolls very slightly 'better' but not to completely break the underlying symmetry and stop the much higher rolls being worse.
- Here's a visual representation of that distribution, but you need to look at the numbers to see subtle shift to larger values:
- 
- Although, it looks like the balance shifts downwards for repeated rolls at the same skill level: https://anydice.com/program/32abe/summary/table
#2: Post edited
by
pureferret
·
2023-10-30T00:19:04Z (7 months ago)
- ## The peak is about 55
- It looks like, based [on this Anydice calculation](https://anydice.com/program/32abc) that peak skill increase is about 55.
- I haven't done an analytical calculation of the probabilities, but my guess is that the initial pass (under) and then the skill advancement check (over) make the distribution symmetric.
- That is a skill level of 5 (where the probability of a success then a subsequent skill advancement is 0.05×0.95=0.0475) is equivalent to when the skill level is 95 (i.e. 0.95×0.05=0.0475), but for a skill level of 50 (i.e. 0.5×0.5=0.25).
- But the probability contribution from both the penalty die, and needing to initially roll under ⅕ the make higher rolls very slightly 'better' but not to completely break the underlying symmetry and stop the much higher rolls being worse.
- Here's a visual representation of that distribution, but you need to look at the numbers to see subtle shift to larger values:
- ## The peak is about 55
- It looks like, based [on this Anydice calculation](https://anydice.com/program/32abc) that peak skill increase is about 55.
- I haven't done an analytical calculation of the probabilities, but my guess is that the initial pass (under) and then the skill advancement check (over) make the distribution symmetric.
- That is a skill level of 5 (where the probability of a success then a subsequent skill advancement is 0.05×0.95=0.0475) is equivalent to when the skill level is 95 (i.e. 0.95×0.05=0.0475), but for a skill level of 50 (i.e. 0.5×0.5=0.25).
- But the probability contribution from both the penalty die, and needing to initially roll under ⅕ the make higher rolls very slightly 'better' but not to completely break the underlying symmetry and stop the much higher rolls being worse.
- Here's a visual representation of that distribution, but you need to look at the numbers to see subtle shift to larger values:
- 
- Although, it looks like the balance shifts downwards for repeated rolls at the same skill level: https://anydice.com/program/32abe
#1: Initial revision
by
pureferret
·
2023-10-29T23:49:54Z (7 months ago)
## The peak is about 55 It looks like, based [on this Anydice calculation](https://anydice.com/program/32abc) that peak skill increase is about 55. I haven't done an analytical calculation of the probabilities, but my guess is that the initial pass (under) and then the skill advancement check (over) make the distribution symmetric. That is a skill level of 5 (where the probability of a success then a subsequent skill advancement is 0.05×0.95=0.0475) is equivalent to when the skill level is 95 (i.e. 0.95×0.05=0.0475), but for a skill level of 50 (i.e. 0.5×0.5=0.25). But the probability contribution from both the penalty die, and needing to initially roll under ⅕ the make higher rolls very slightly 'better' but not to completely break the underlying symmetry and stop the much higher rolls being worse. Here's a visual representation of that distribution, but you need to look at the numbers to see subtle shift to larger values: 